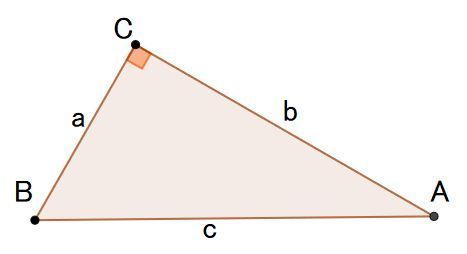
重要 三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b とし、斜辺の長さを c とすると、次の関係が成り立つ。 c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} この定理を証明したのは古代ギリシアの数学者ピタゴラスであるとも言われているので、この · ^ a b c "三平方の定理の逆の証明" 14年10月8日 閲覧。 ^ 不定積分の漸化式 ^ a b "三平方の定理の証明" 14年10月5日 閲覧。 ^ "Einige spezielle Funktionen" 14年11月26日 閲覧。 ^ Hamilton, James Douglas (1994) "Power series" Time四平方の定理 (1)発見に至るまで 立体の基本図形として、立方体の一部を切り取ってできる合同な3枚の直角三角形と1枚の正三角形からなる三角錐を考えた。 頂点Oを通るコマの軸は、底面 ABCに垂直になる。 直方体から切り取った三角錐では、頂点から
三石 数学塾 三平方の定理の証明 その2
三平方の定理 証明 一覧
三平方の定理 証明 一覧-三平方の定理の証明方法を説明する 三平方の定理を使って正方形の面積の和を考える 三平方の定理を使って辺の長さを求める 相似と三平方の定理を使って長さを求める 長方形やひし形の対角線の長さを求める 台形の対角線の長さや面積を求める三平方の定理直角三角形辺の長さ 四平方の定理直角三角錐面の面積 三平方の定理は, 直角三角形において,斜辺の平方は直角をはさむ2辺の平方の和に等しい と表現される. 四平方の定理を同様に表現すると,



三平方の定理
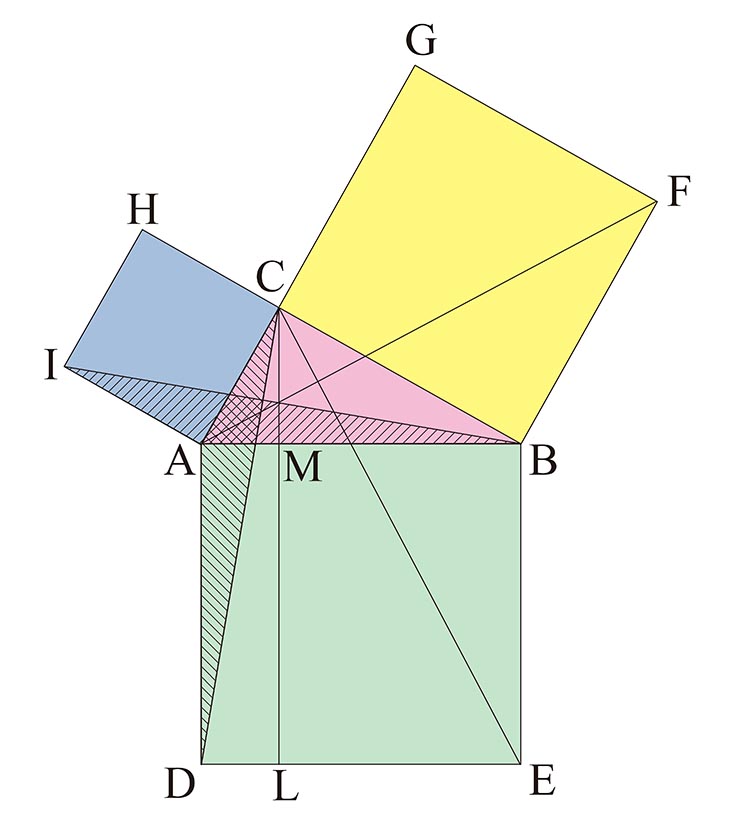
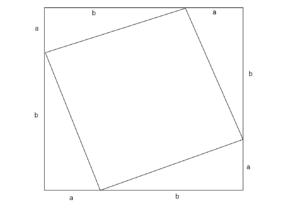
三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べて正方形ABDFをつくる。 正方形ABDFの面積をSとすると、1辺がcなので S=c2 ① また、正方形ABDFは△ABCと合同な三角形4つと正方形EGHCでできている。三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵 が成り立つことを、 三平方の定理 と言います。 三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが 3 c m と 4 c m の直角三角形三 平方 の 定理 直角 三角形 Pictngamukjp5mhn 直角三角形において、「直角」をはさむ2つの辺の長さを \ (a,b\)、斜辺の長さを \ (c\) としたとき 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵|アタリマエ!3
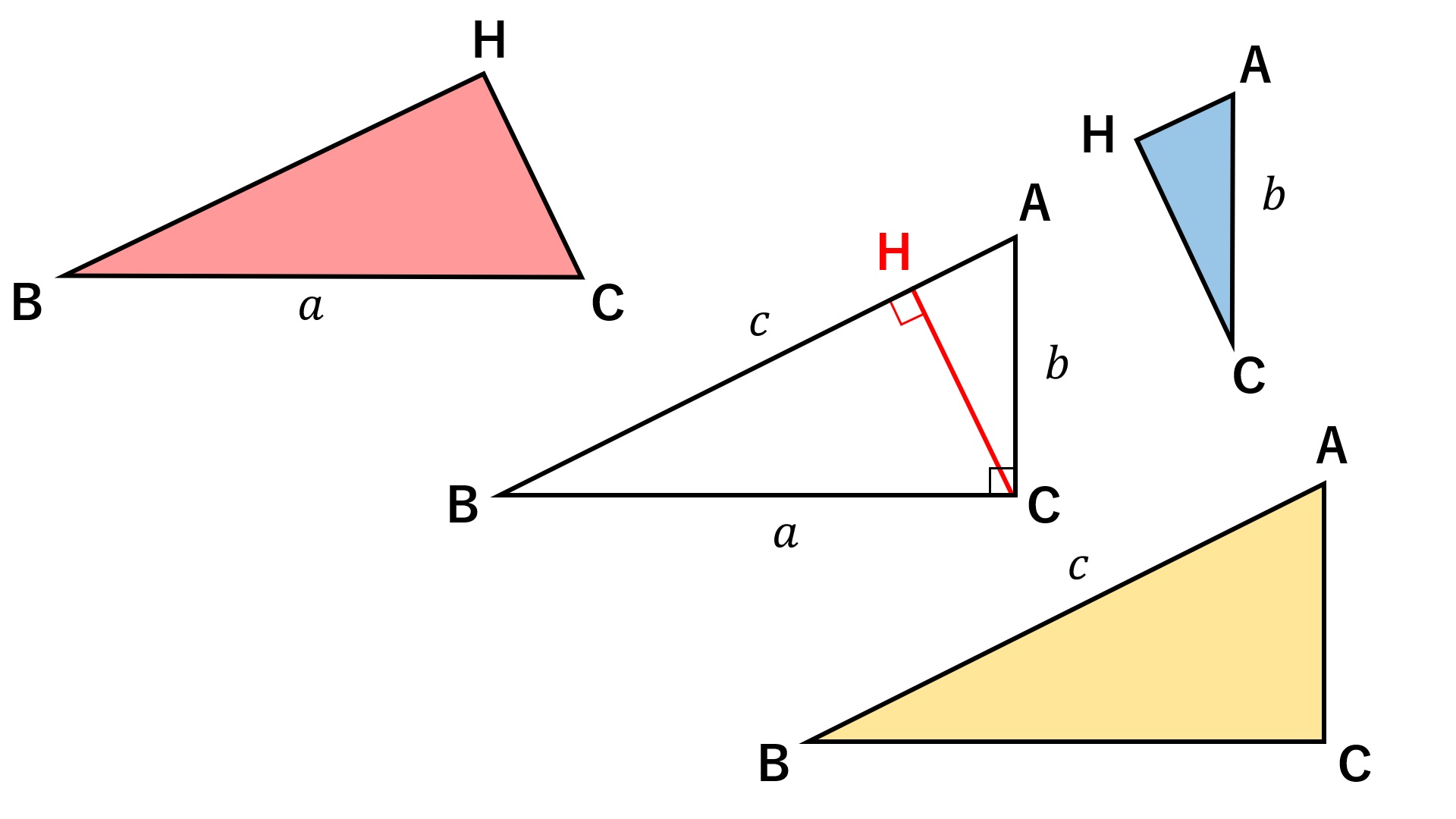
四平方の定理 角oが全て直角の直角四面体oabcにおいて、面積について s 1 2 s 2 2 s 3 2 = s 4 2 が成り立つ。ピタゴラスの定理とその証明 中学3年で学習するピタゴラスの定理(三平方の定理)は、その後の数学の学習で繰り 返し用いられる重要な定理である。 ピタゴラスの定理(三平方の定理) 左図のような直角三角形ABCにおいて、 a2+b2=c2 が成り立つ。 逆に、上式が成り立つような3辺 a,b,c をもつ三 角形は直角三角形である。三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 a b
· 三平方の定理の証明 三平方の定理とは以下のように直角三角形ABCがあった時に、辺a(底辺)と辺b(高さ)の2つと辺c(斜辺)の関係性を以下のような等式で表した定理です。 公式:a²+b²=c² わかりやすく文章で表現しますと、 底辺の2乗と高さの2乗の和が斜辺の2乗に等しい ことです。 二乗になるので最終的には 平方根 (√)をつければ斜辺が求まります · 証明や計算問題、角度と辺の比の一覧 この記事では「三平方の定理」について、その公式や計算方法をできるだけわかりやすく解説していきます。 また、三平方の定理の証明や実際の問題なども紹介していきますので、この記事を通してぜひマスターして初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem)は、直角三角形の3辺の長さの関係を表す。斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は c 2 = a 2 b 2 {\displaystyle c^{2}=a^{2}b^{2}} が成り立つという等式の形で述べられる。三平方の定理(さんへいほうのていり)、勾股弦の定理(こうこげんのていり)とも呼ばれる。 ピタゴラス




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ




中学数学 三平方の定理
平方根の乗除① 平方根を簡単にする 652 平方根の乗除② 練習問題 727 5平方根の有理化 平方根の有理化 609 中点連結定理の利用① 証明 726 中点連結定理の利用② 線分の長さ 804 4発展三角形の重心 三角形の重心 906 · 更新日時 三平方の定理(ピタゴラスの定理): ∠ C = 9 0 ∘ \angle C=90^ {\circ} ∠C = 90∘ であるような直角三角形において, a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。 →Pythagorean Theorem三平方の定理の逆ってなに? 三平方の定理を文字で起こしてみるとこんな感じ。 3辺の長さ 斜辺 とする直角三角形ならば、 が成り立つ これを逆にしたものを 3辺の長さが の三角形において が成り立つならば、 ABCはcを斜辺とする直角三角形となる



三平方の定理




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ
ありません。三平方の定理の逆の証明として,間接証明法である同一法がありますが,直接証明法ではない証明 法があることを知る機会として,証明の全体の流れを理解できる程度に扱うとよいでしょう。 三平方の定理の逆の証明について 中学数学 3年3-1②ピタゴラスの定理の証明 proof of Pythagorean theorem 三平方の定理(ピタゴラス) ピタゴラスの定理(ユークリッドの証明) · GaussLegendreの三平方の定理は平方剰余の相互法則、Dirichletの算術級数定理、Minkowskiの凸体定理、二平方和の定理と初等整数論における一級の定理達を総動員して証明されます。 命題 4k(8l 7) ( k, l は非負整数)の形をした正整数は三つの平方数の和として表す




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



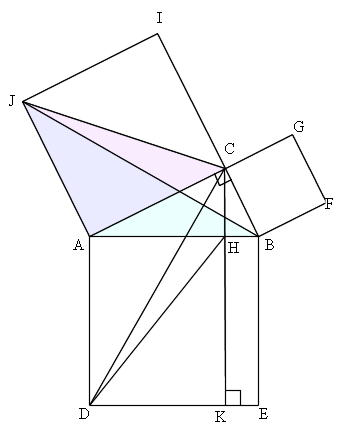
三平方の定理の証明 ピタゴラスの定理とはあまり言いたくない キソカラ
= (1)p 21 8 p とa、p とb が素であれば、 ab p!三平方の定理の証明5選直角三角形や正方形を重ねましょう 三平方の定理(別名ピタゴラスの定理)とは、底辺が $a$、高さが $b$、斜辺が $c$ である直角三角形において、$$a^2b^2=c^2$$ が成り立つことでしたね。四平方和定理 (英语:Lagrange's foursquare theorem) 说明每个正整数均可表示为4个整数的平方和。它是费马多边形数定理和华林问题的特例。注意有些整数不可表示为3个整数的平方和,例如7。



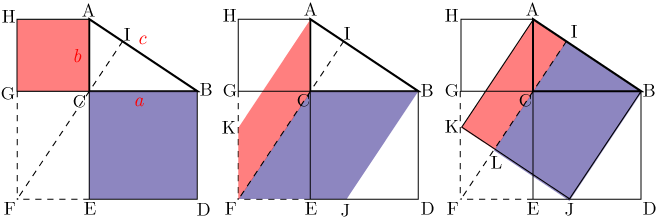
Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ



三平方の定理 ピタゴラスの定理
美しい 三 平方 の 定理 証明 中学生 三平方の定理について考える1 教科書 大日本図書 の証明方法 中学数学 三平方の定理 証明 図形的に オンライン無料塾円の基本的な性質 弦、接線、接点という言葉は覚えていますか? その図形的性質は覚えていますか?相対性理論で有名なアインシュタインによる「ピタゴラスの定理(三平方の定理)」の証明です。PYTHAGOREAN THEOREM Proof by Albert Einstein#1レオナルド自然数 が三個の平方数の和で表されるための必要十分条件は、,, {,,,,} により、 = () と表されることである。 逆に、 = () で表される自然数は三個の平方数の和で表されない。 これはディオファントスの時代から研究されてきた ことであるが、1798年、ルジャンドルによって証明された。




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
· ピタゴラスの定理(三平方の定理)を使うと, a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 を満たす自然数の組 (a, b, c) (a,b,c) (a, b, c) をピタゴラス数と呼ぶ。 と言うこともできます。 例えば, 3 2 4 2 = 5 2 3^24^2=5^2 3 2 4 2 = 5 2 なので (3, 4, 5) (3,4,5) (3, 4, 5) はピタゴラス数です。 他にも, 5 2 1 2 2 = 1 3 2 5^212^2=13^2 5 2 1 2 2 = 1 3 2定理13 (第1 補充法則) p は奇素数とする、このとき次が成立する。 1 p!= (1)p1 2 定理14 (第2 補充法則) p は奇素数とする、このとき次が成立する。 2 p!



三平方の定理 アメリカ合衆国大統領の証明 数々のたのしみ




三平方の定理の証明と使い方
数学 三平方の定理の証明と使い方 三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。 ここで、斜辺とは、直角三角形の直角に対する対辺のことです。 三平方の定理は、別名、 ピタゴラスの定理 とも呼ばれます。 三平方の定理(ピタゴラスの定理) 3 辺の長さが a, b, c の三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。中線定理の証明 これを証明してみましょう。 まず、頂点aから辺bcに垂線を下ろし、その交点をhとします。 abhに三平方の定理をあては無料印刷可能 三 平方 の 定理 証明 一覧 三平方の定理の証明 ピタゴラスの定理とはあまり言いたくない




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも
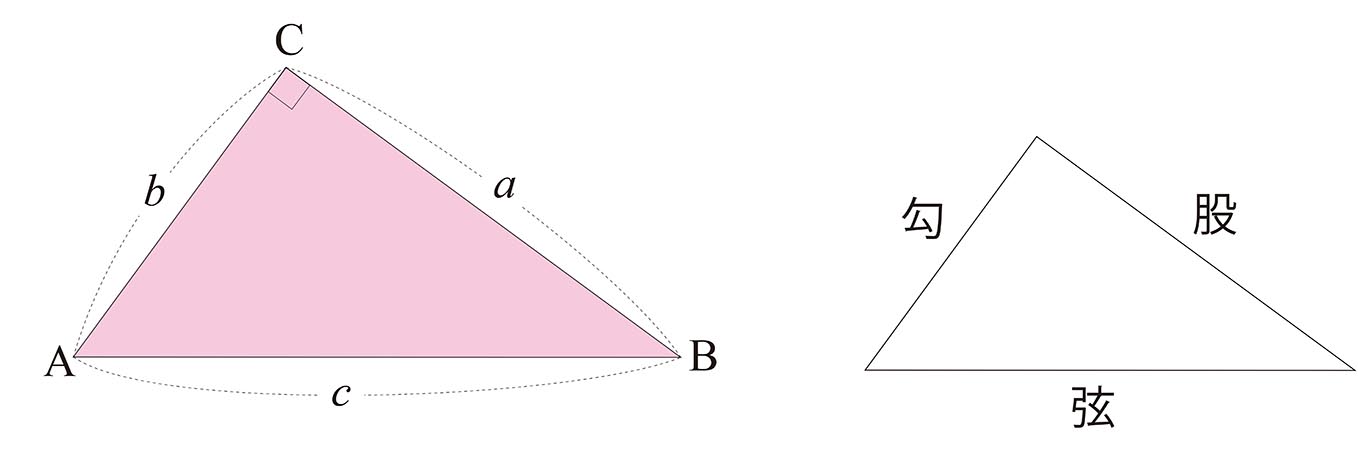



コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション
· 英訳:Description of the wonderful canon of logarithms 日本語訳:奇跡の対数法則の記述 ロガリズム(logarithms) という言葉は、この時ネイピアによって考案された造語です。 logos(神の言葉) とギリシャ語の arithmos(数) を合わせて logarithms という言葉を作りました。 ネイピアは自らの著書を「 奇跡 」と呼びました。 対数が「 人の命を救う 」だけの力を持ってい从 1730 年至 1770 年, 在大约四十年的时间里 Euler 证明了许多与四平方定理有关的结果, 为后来这一定理的证明创造了条件, 但他本人却很遗憾地未能率先证明这一定理 注三 。 1770 年, 法国数学家 Joseph Lagrange () 以 Euler 的一个结果为基础, 率先给出了三平方の定理は、直角三角形の3つの辺の長さの関係を表わした定理で、直角三角形の直角を挟む2つの辺の長さをそれぞれ a a 、 b b とし、斜辺の長さを c c とすると、 a2 b2 = c2 a 2 b 2 = c 2 の関係が成り立つ、という定理です。



コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション



ピタゴラスの定理とその証明
· 三個の平方数の和 三個の平方数の和の概要 自然数が三個の平方数の和で表されるための必要十分条件は、により、と表されることである。逆に、で表される自然数は三個の平方数の和で表されない。これはディオファントスの時代から研究されてきた1ことであこの定理の逆も成り立つ。すなわち、三角形の1辺の平方が他の2辺の平方の和に等しければ、始めの辺に対する頂角は直角である。この逆定理の成立によって、たとえば、辺の長さが3、4、5である三角形は3 2 +4 2 =5 2 であるから、直角三角形となる。この3 · 2平方定理この定理はフェルマーの2平方定理とも呼ばれることがあり,証明はオイラーによってはじめてなされたとされています.定理.奇素数(奇数かつ素数,すなわち 3 以上の素数) \(p\) が 4 で割ると 1 余るとき,\(p\) は 2




三平方の定理 ピタゴラスの定理 と証明 Rikeinvest



ピタゴラスの定理 Wikipedia
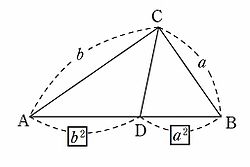
三平方の定理とは? / 三平方の定理の逆 / 有名角と比 / 2点間の距離 / 円の中心と弦との距離 / 空間図形の対角線・高さ / 空間図形とひもの最短距離中線定理の証明 これを証明してみましょう。 まず、頂点Aから辺BCに垂線を下ろし、その交点をHとします。 ABHに三平方の定理をあてはめると、 ① ACHに三平方の定理をあてはめると、 ② ①+②より ③ 一方で、BH=BM+MH、CH=CM-MH、またBM=CMより



三平方の定理 理系ノート




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



1




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




ピタゴラス数が一発でわかる公式 証明もあわせて解説 遊ぶ数学



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




数学 中3 61 三平方の定理 基本編 Youtube




数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月
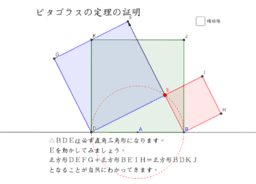



ピタゴラスの定理 三平方の定理 の証明 Geogebra



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典
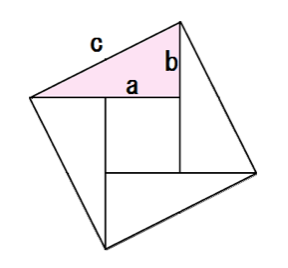



中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく



三平方の定理




ある三平方の定理の証明方法 中学校程度の数学で理解しよう 身勝手な主張




三平方の定理の証明 直感的に分かる図で解説します 数学fun




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
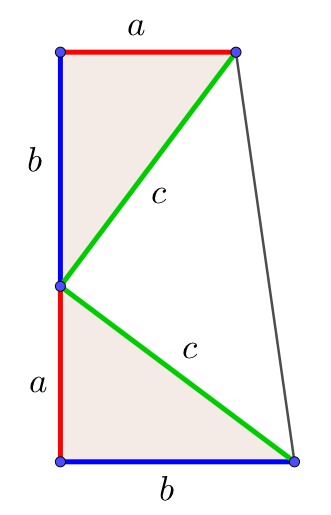



三平方の定理の証明3 大統領の台形 キソカラ




三平方の定理の証明 相似を利用した証明2 Fukusukeの数学めも
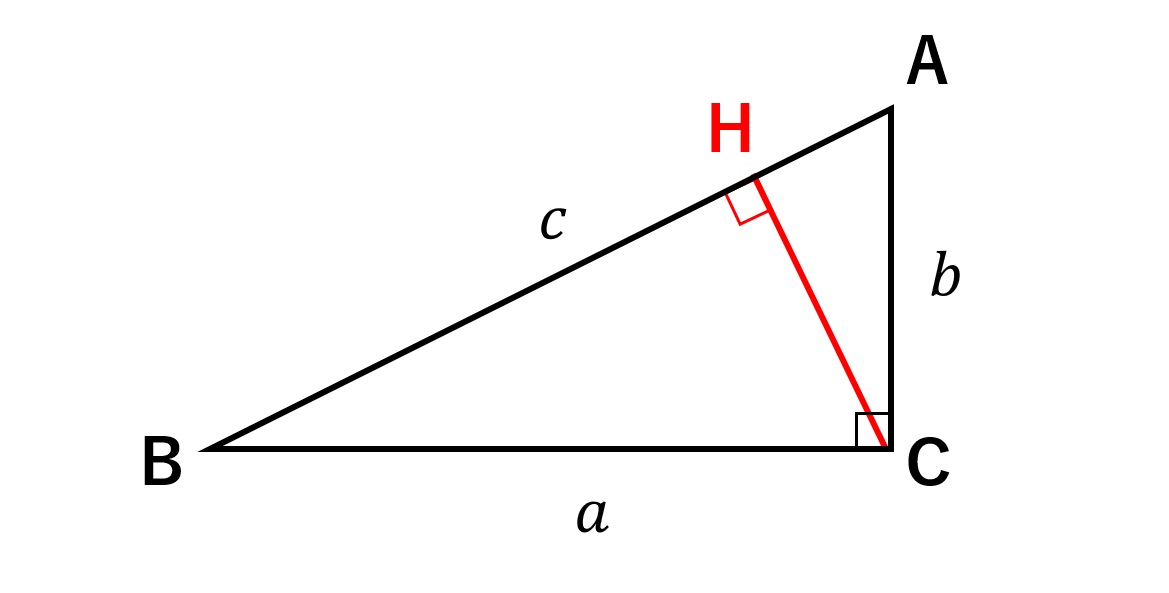



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




Catatan Tentang 中学数学 三平方の定理のキホン Junior Clear




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



1




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張




ピタゴラスの定理 Wikipedia




コラム ピタゴラスの定理 江戸の数学




3 4 5の三角形で 本当に直角ができる Note Board
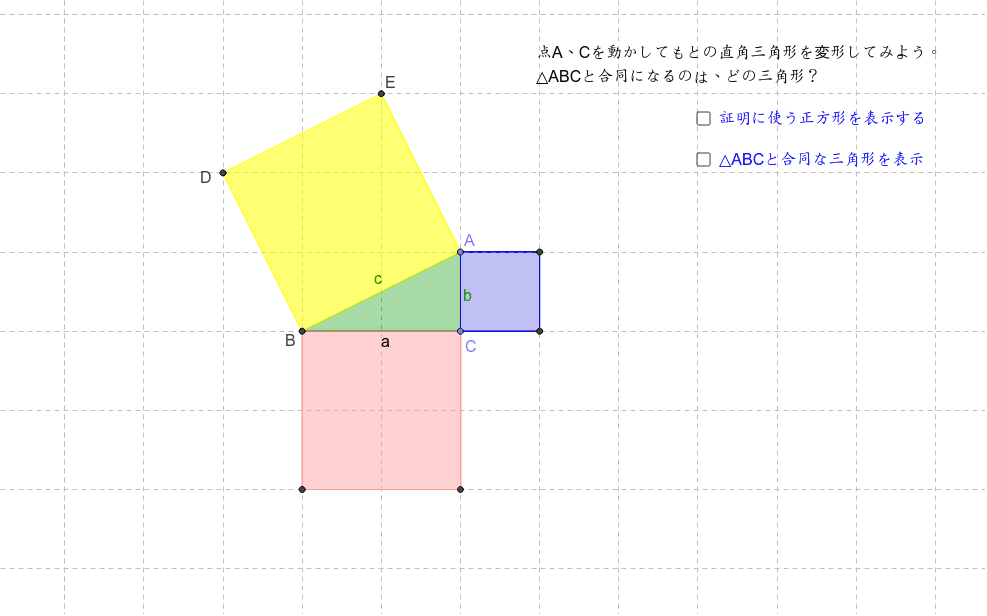



三平方の定理のある証明で使われる図 Geogebra



三石 数学塾 三平方の定理の証明 その2



三平方の定理




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



1




三平方の定理の4通りの美しい証明 高校数学の美しい物語
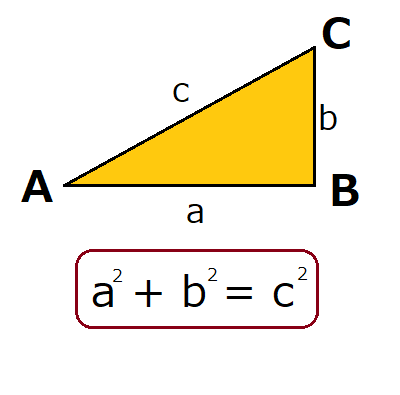



三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋




三平方の定理を証明せよ 中学生課題 ふるやまんのマスラボ奮闘記



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




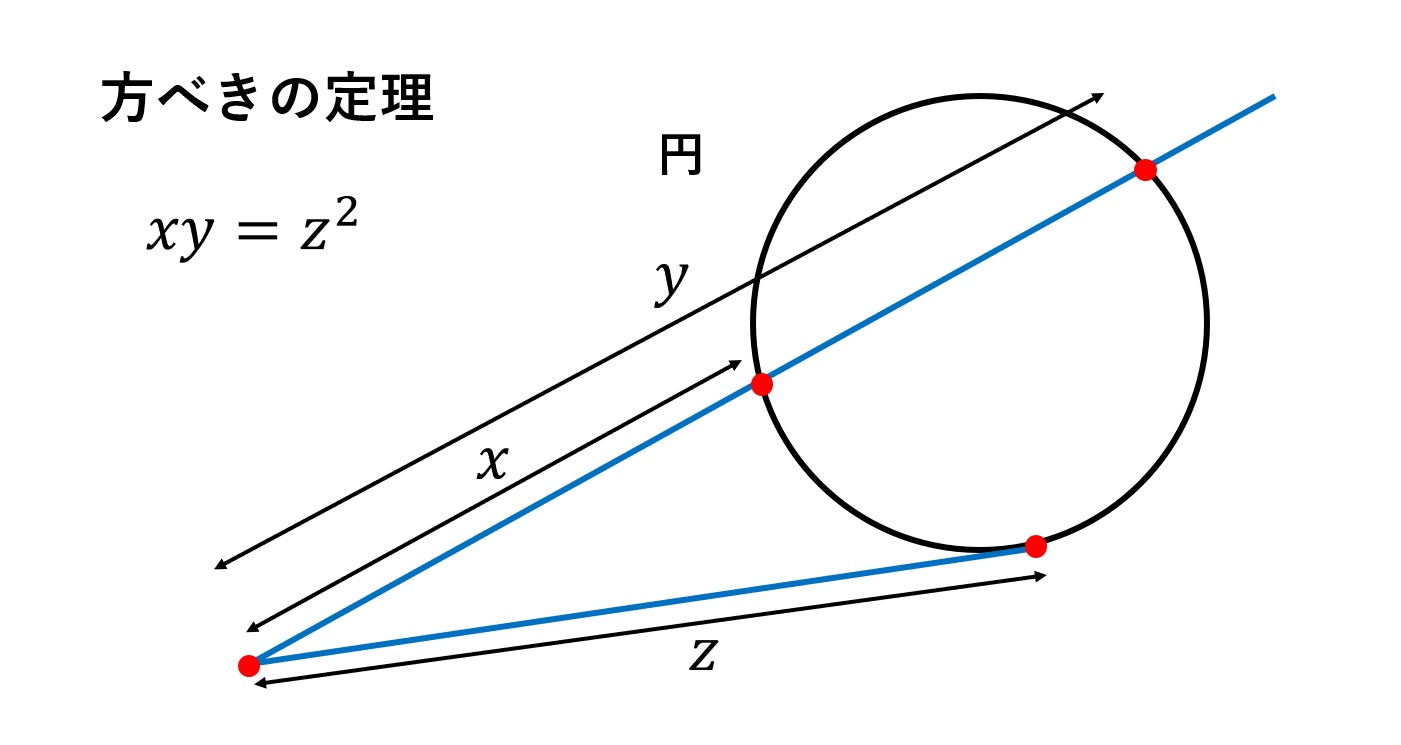
方べきの定理を使った三平方の定理の証明2 数学のすすめ



三平方の定理




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理の4通りの美しい証明 高校数学の美しい物語




ピタゴラスの定理 Wikipedia




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




三平方の定理の証明 方べきの定理の利用1 Fukusukeの数学めも




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook
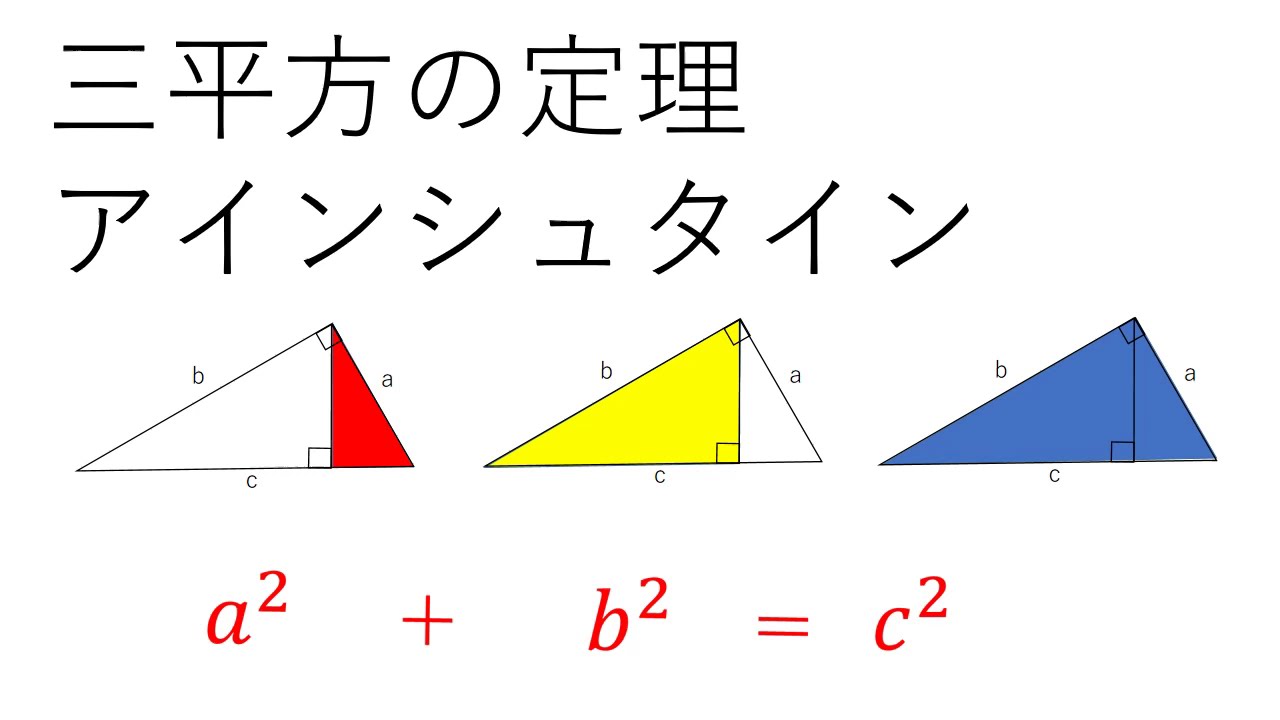



三平方の定理8 アインシュタイン Youtube




余弦定理 は三平方の定理の進化版 余弦定理は2つある
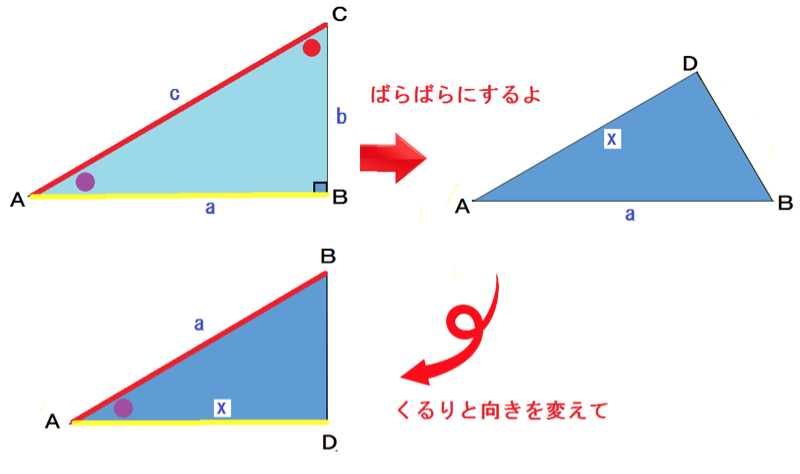



中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく




三平方の定理 覚えておきたい基本公式を解説 数スタ




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
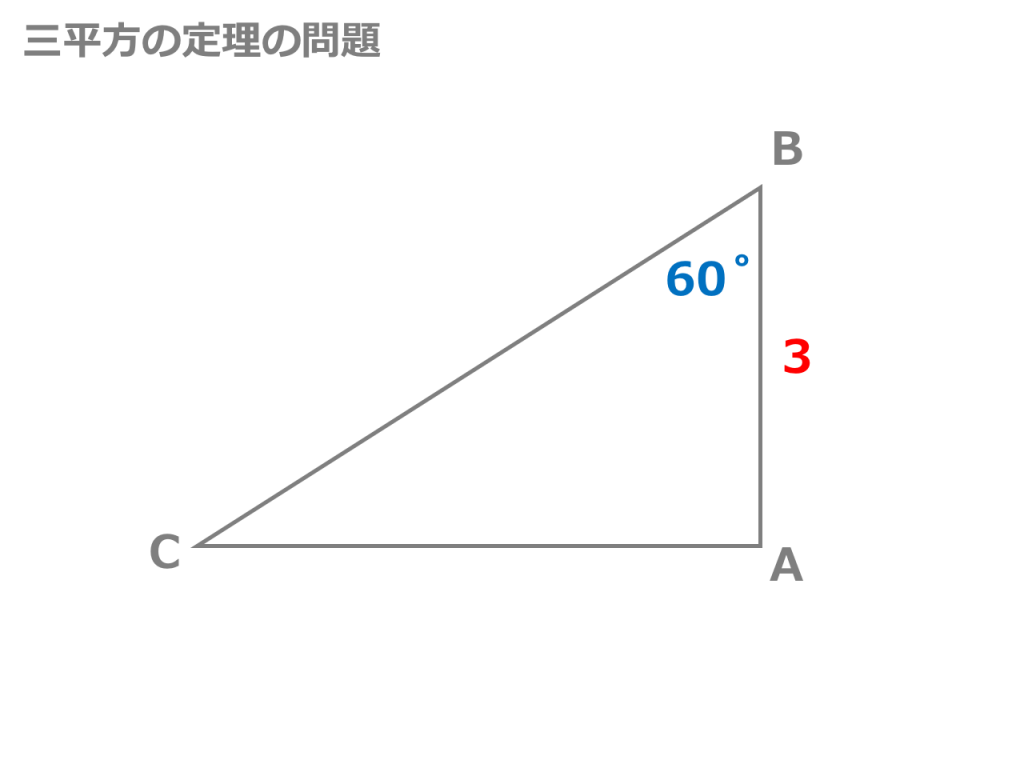



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ
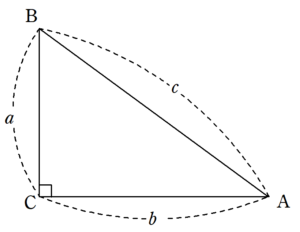



三平方の定理の証明 アン コンディットの証明 Fukusukeの数学めも




三平方の定理の4通りの美しい証明 高校数学の美しい物語
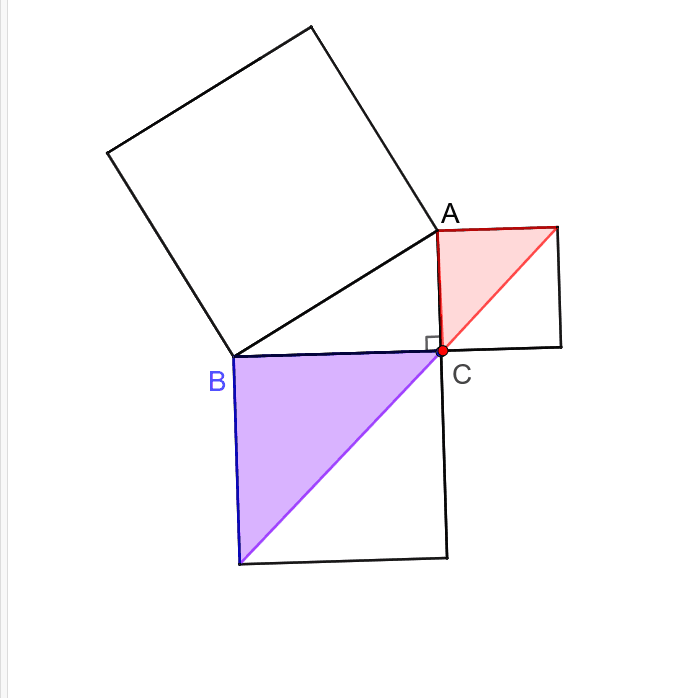



三平方の定理の証明 ユークリッドの証明 Geogebra




三平方の定理の証明 の宇宙




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
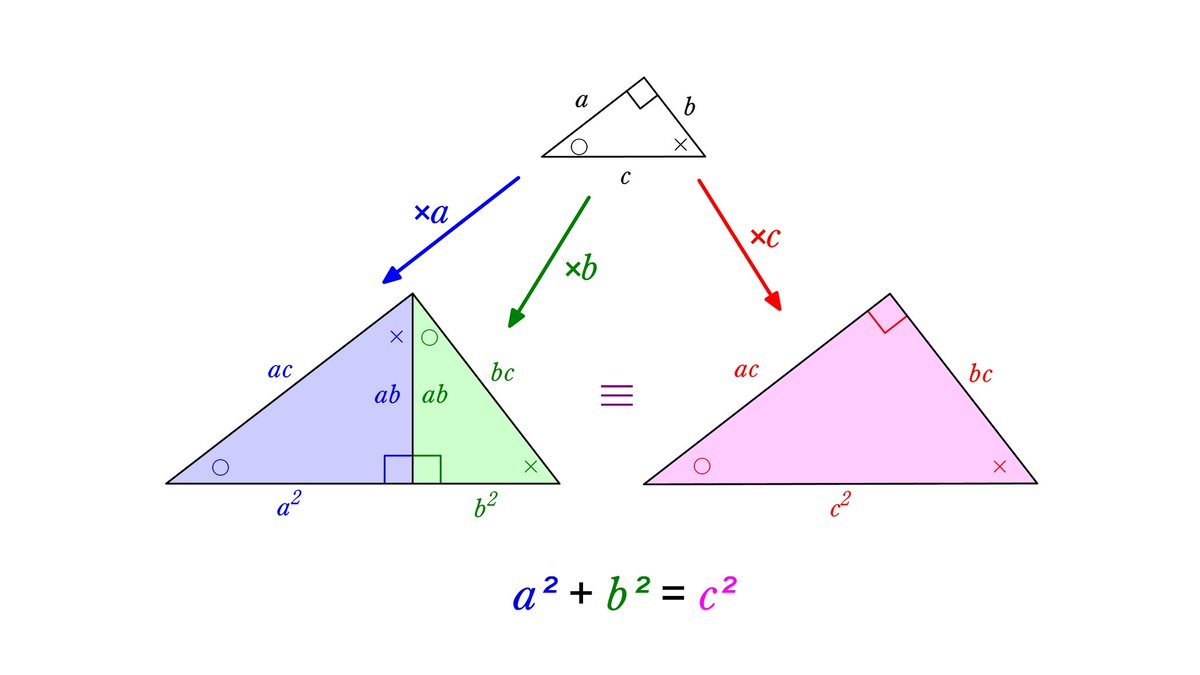



ポテト一郎 三平方の定理 一番好きな証明です
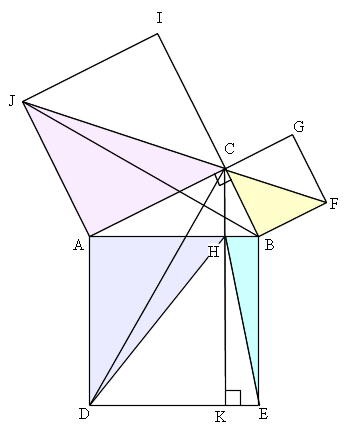



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ
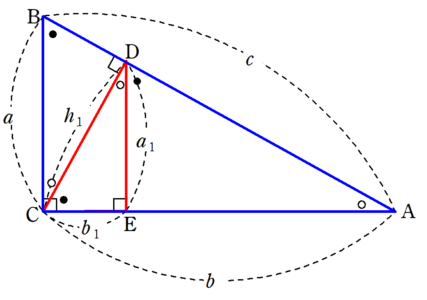



三平方の定理の証明 無限等比級数を利用した証明 Fukusukeの数学めも
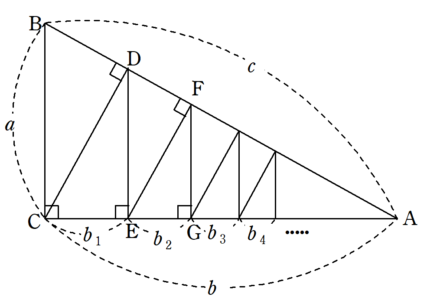



三平方の定理の証明 無限等比級数を利用した証明 Fukusukeの数学めも



ピタゴラスの定理 三平方の定理 の証明ついて 未設定




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ The 2nd
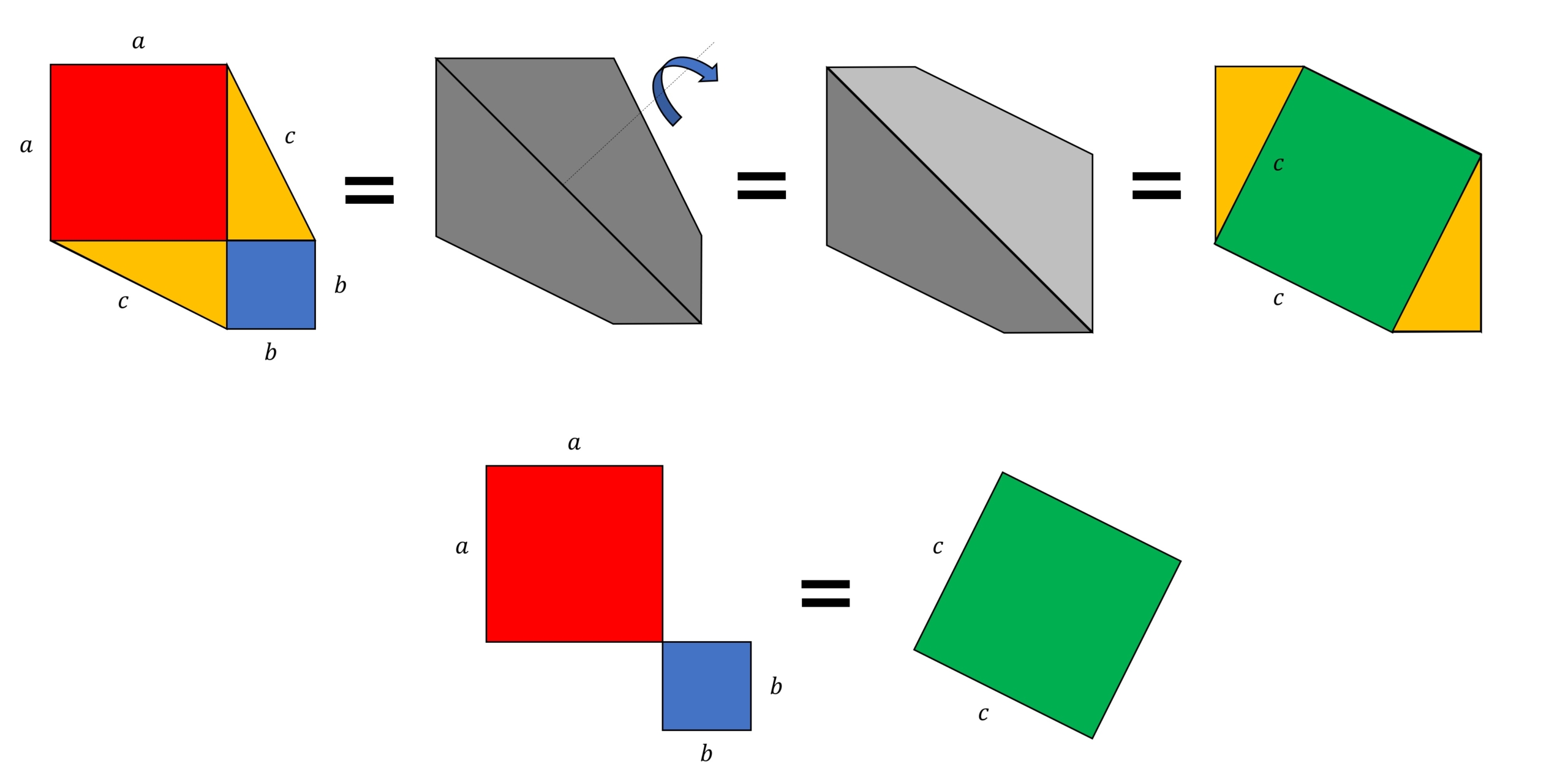



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



1



Studydoctor三平方の定理の証明 中学3年数学 Studydoctor




三平方の定理の証明と使い方
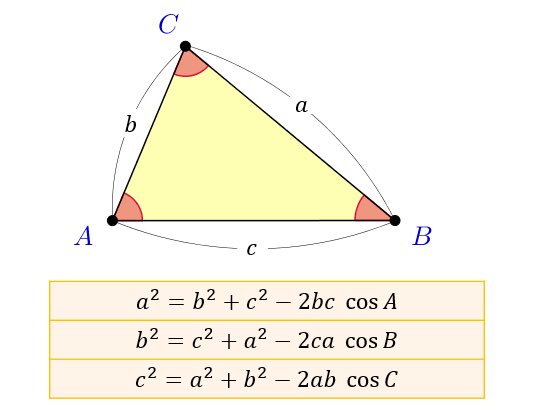



けんちょん そして 三平方の定理 の一般化であるはずの余弦定理 それ自体を 三平方の定理 を使って 証明することができます ある定理を一般化を その定理自体を使って示すことができる みたいな状況は 数学やってると結構ある
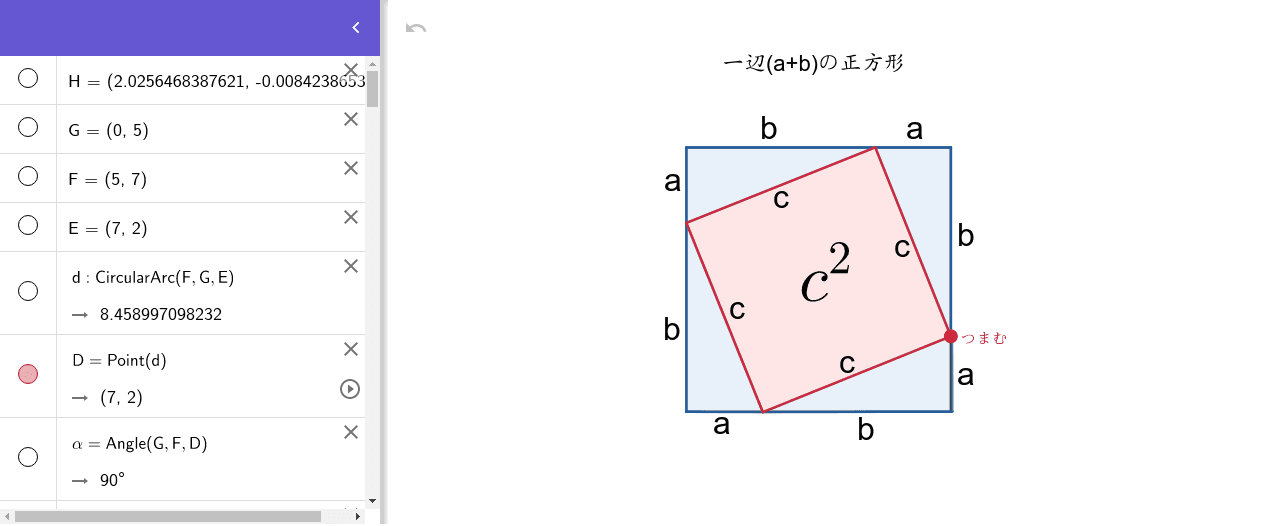



三平方の定理 証明 Geogebra



中3数学 三平方の定理1 三平方の定理 証明 すべて無料 星組の中学数学講座



三平方の定理
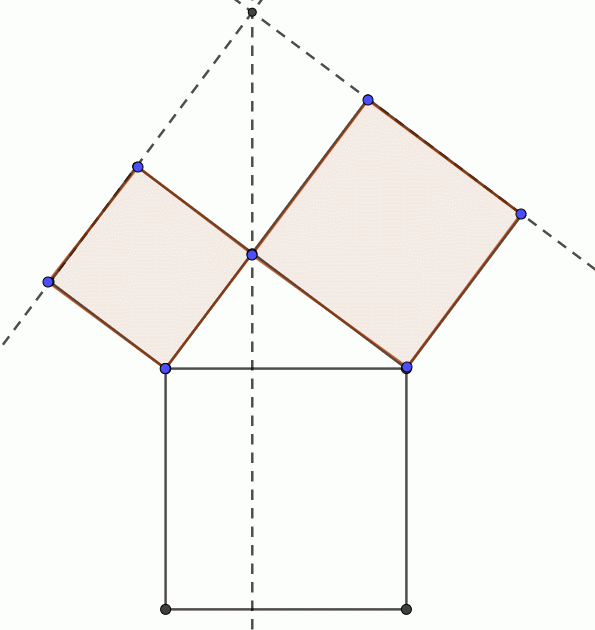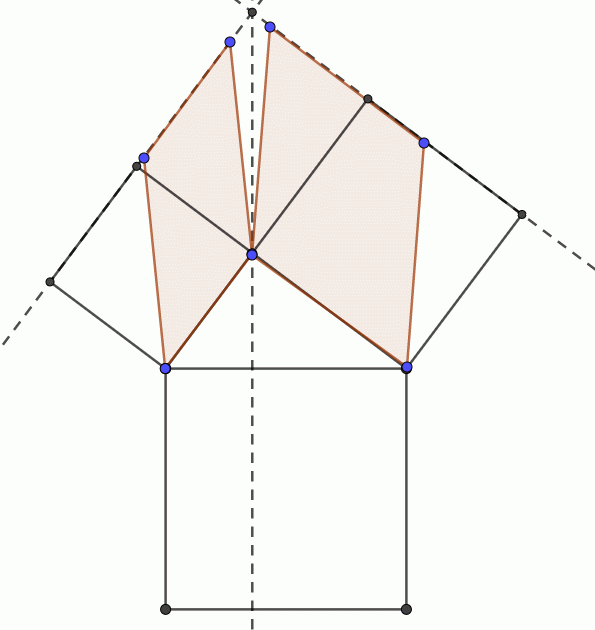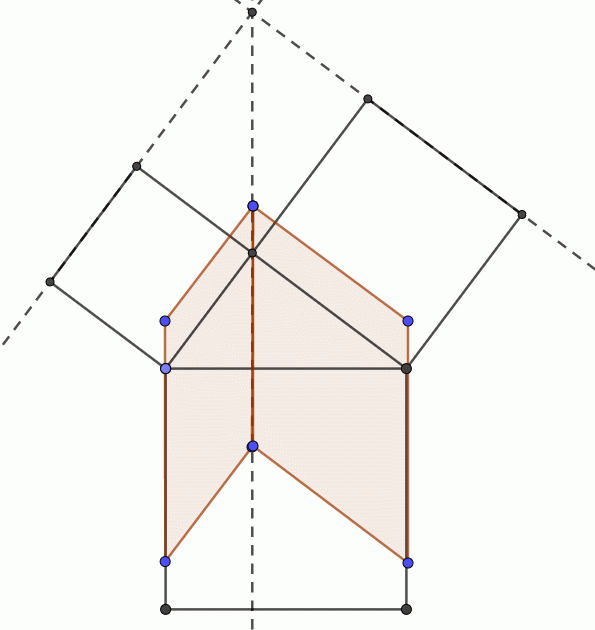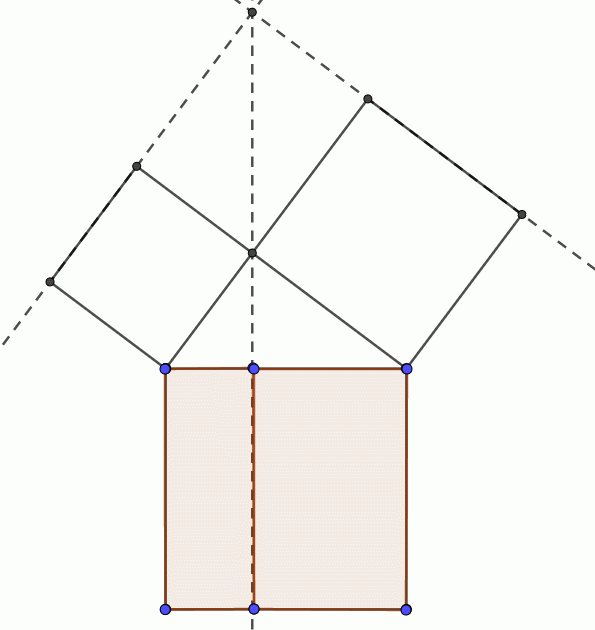



三平方の定理の証明5 だまって平行移動 キソカラ



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Pc Mathekyouzai001 Sanheihou Theorem Pdf
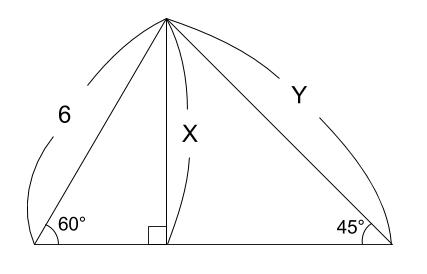



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



三平方の定理



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理の証明と使い方
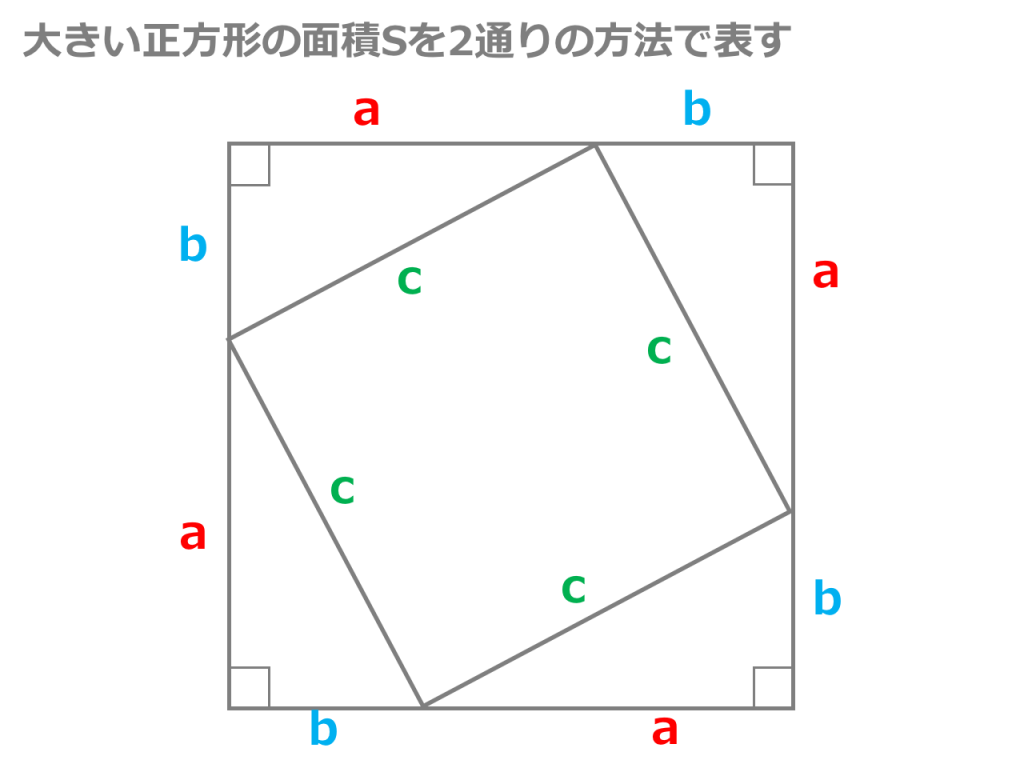



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
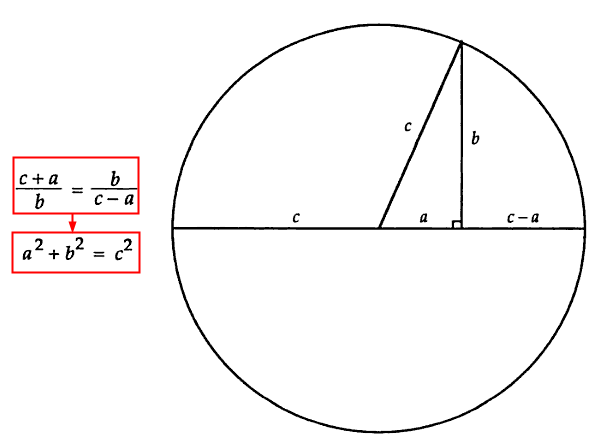



数学の概念 を視覚的かつ美しく表現したグラフィックいろいろ Gigazine




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
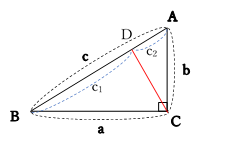



三平方の定理 おやじさん ネット



0 件のコメント:
コメントを投稿